Let
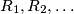
be the family of finite sequences of positive integers defined by the following rules:
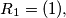
and if
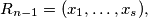
then
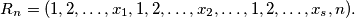
For example,
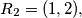
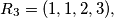
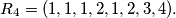
Prove that if
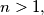
then the

th term from the left in
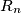
is equal to 1 if and only if the

th term from the right in
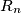
is different from 1.
%V0
Let $R_1,R_2, \ldots$ be the family of finite sequences of positive integers defined by the following rules: $R_1 = (1),$ and if $R_{n - 1} = (x_1, \ldots, x_s),$ then
$$R_n = (1, 2, \ldots, x_1, 1, 2, \ldots, x_2, \ldots, 1, 2, \ldots, x_s, n).$$
For example, $R_2 = (1, 2),$ $R_3 = (1, 1, 2, 3),$ $R_4 = (1, 1, 1, 2, 1, 2, 3, 4).$ Prove that if $n > 1,$ then the $k$th term from the left in $R_n$ is equal to 1 if and only if the $k$th term from the right in $R_n$ is different from 1.