On a semicircle with unit radius four consecutive chords
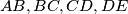
with lengths
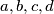
, respectively, are given. Prove that
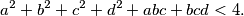
%V0
On a semicircle with unit radius four consecutive chords $AB,BC, CD,DE$ with lengths $a, b, c, d$, respectively, are given. Prove that
$$a^2 + b^2 + c^2 + d^2 + abc + bcd < 4.$$