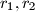
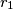
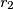
We are given two mutually tangent circles in the plane, with radii . A line intersects these circles in four points, determining three segments of equal length. Find this length as a function of and and the condition for the solvability of the problem.
%V0
We are given two mutually tangent circles in the plane, with radii $r_1, r_2$. A line intersects these circles in four points, determining three segments of equal length. Find this length as a function of $r_1$ and $r_2$ and the condition for the solvability of the problem.
Izvor: Međunarodna matematička olimpijada, shortlist 1971
Školjka 
. A line intersects these circles in four points, determining three segments of equal length. Find this length as a function of 
and 
and the condition for the solvability of the problem.