An international society has its members from six different countries. The list of members contain 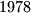 names, numbered
names, numbered 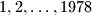 . Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
. Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
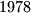 names, numbered
names, numbered 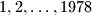 . Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.
. Prove that there is at least one member whose number is the sum of the numbers of two members from his own country, or twice as large as the number of one member from his own country.  Školjka
Školjka