Let

and

be opposite vertices of an octagon. A frog starts at vertex
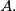
From any vertex except

it jumps to one of the two adjacent vertices. When it reaches

it stops. Let

be the number of distinct paths of exactly

jumps ending at

. Prove that:
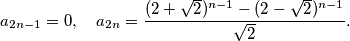
%V0
Let $A$ and $E$ be opposite vertices of an octagon. A frog starts at vertex $A.$ From any vertex except $E$ it jumps to one of the two adjacent vertices. When it reaches $E$ it stops. Let $a_n$ be the number of distinct paths of exactly $n$ jumps ending at $E$. Prove that: $$a_{2n-1}=0, \quad a_{2n}={(2+\sqrt2)^{n-1} - (2-\sqrt2)^{n-1} \over\sqrt2}.$$