Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 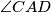 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.
 i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 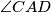 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.  Školjka
Školjka