Determine all real values of the parameter

for which the equation
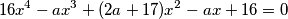
has exactly four distinct real roots that form a geometric progression.
%V0
Determine all real values of the parameter $a$ for which the equation
$$16x^4 -ax^3 + (2a + 17)x^2 -ax + 16 = 0$$
has exactly four distinct real roots that form a geometric progression.