Let  be a square with sides length
be a square with sides length 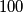 . Let
. Let  be a path within
be a path within  which does not meet itself and which is composed of line segments
which does not meet itself and which is composed of line segments 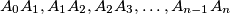 with
with 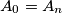 . Suppose that for every point
. Suppose that for every point  on the boundary of
on the boundary of  there is a point of
there is a point of  at a distance from
at a distance from  no greater than
no greater than  . Prove that there are two points
. Prove that there are two points  and
and  of
of  such that the distance between
such that the distance between  and
and  is not greater than
is not greater than  and the length of the part of
and the length of the part of  which lies between
which lies between  and
and  is not smaller than
is not smaller than 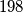 .
.
 be a square with sides length
be a square with sides length 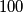 . Let
. Let  be a path within
be a path within  which does not meet itself and which is composed of line segments
which does not meet itself and which is composed of line segments 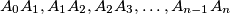 with
with 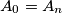 . Suppose that for every point
. Suppose that for every point  on the boundary of
on the boundary of  there is a point of
there is a point of  at a distance from
at a distance from  no greater than
no greater than  . Prove that there are two points
. Prove that there are two points  and
and  of
of  such that the distance between
such that the distance between  and
and  is not greater than
is not greater than  and the length of the part of
and the length of the part of  which lies between
which lies between  and
and  is not smaller than
is not smaller than 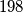 .
.  Školjka
Školjka