Let
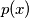
be a cubic polynomial with integer coefficients with leading coefficient
and with one of its roots equal to the product of the other two. Show that
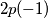
is a multiple of
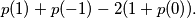
%V0
Let $p(x)$ be a cubic polynomial with integer coefficients with leading coefficient $1$ and with one of its roots equal to the product of the other two. Show that $2p(-1)$ is a multiple of $p(1)+p(-1)-2(1+p(0)).$
Školjka