Slični zadaci
Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 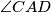 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.
 i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 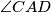 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.  Školjka
Školjka 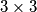 treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude
treba upisati prirodne brojeve, tako da u svakom retku i svakom stupcu produkt upisanih brojeva bude 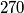 . Na koliko je načina to moguće napraviti?
. Na koliko je načina to moguće napraviti?  i
i  šiljastokutnog trokuta
šiljastokutnog trokuta  s vanjske strane konstruiraju se kvadrat
s vanjske strane konstruiraju se kvadrat 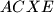 i
i 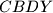 . Dokažite da se pravci
. Dokažite da se pravci  i
i  sijeku na visini iz vrha
sijeku na visini iz vrha  i
i  prirodni brojevi. Dokažite da nejednakost
prirodni brojevi. Dokažite da nejednakost
 i
i  ako i samo ako je
ako i samo ako je  .
.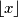 je oznaka za najveći cijeli broj koji nije veći od
je oznaka za najveći cijeli broj koji nije veći od  .)
.)  stranice duljine
stranice duljine  , dane su točke
, dane su točke 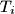 ,
, 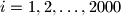 , tako da nikoje tri točke u skupu
, tako da nikoje tri točke u skupu 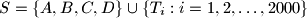 nisu kolinearne. Dokažite da postoji barem jedan trokut, s vrhovima u skupu
nisu kolinearne. Dokažite da postoji barem jedan trokut, s vrhovima u skupu  , površine manje od
, površine manje od 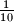 .
.  dira stranicu
dira stranicu  i
i  ,
,  . Dužine
. Dužine 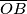 i
i 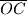 sijeku spojnicu
sijeku spojnicu 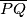 redom u točkama
redom u točkama 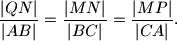
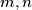 za koje vrijedi
za koje vrijedi