Slični zadaci
A non-isosceles triangle 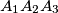 has sides
has sides 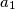 ,
, 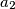 ,
, 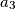 with the side
with the side 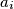 lying opposite to the vertex
lying opposite to the vertex 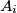 . Let
. Let 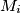 be the midpoint of the side
be the midpoint of the side 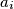 , and let
, and let 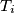 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 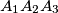 touches the side
touches the side 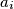 . Denote by
. Denote by 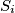 the reflection of the point
the reflection of the point 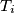 in the interior angle bisector of the angle
in the interior angle bisector of the angle 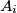 . Prove that the lines
. Prove that the lines 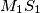 ,
, 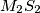 and
and 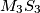 are concurrent.
are concurrent.
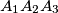 has sides
has sides 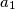 ,
, 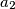 ,
, 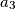 with the side
with the side 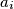 lying opposite to the vertex
lying opposite to the vertex 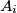 . Let
. Let 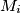 be the midpoint of the side
be the midpoint of the side 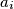 , and let
, and let 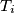 be the point where the inscribed circle of triangle
be the point where the inscribed circle of triangle 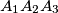 touches the side
touches the side 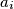 . Denote by
. Denote by 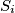 the reflection of the point
the reflection of the point 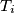 in the interior angle bisector of the angle
in the interior angle bisector of the angle 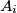 . Prove that the lines
. Prove that the lines 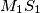 ,
, 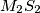 and
and 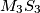 are concurrent.
are concurrent. Let  and consider a set
and consider a set  of
of 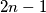 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good.
 and consider a set
and consider a set  of
of 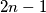 distinct points on a circle. Suppose that exactly
distinct points on a circle. Suppose that exactly  of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly
of these points are to be colored black. Such a coloring is good if there is at least one pair of black points such that the interior of one of the arcs between them contains exactly  points from
points from  . Find the smallest value of
. Find the smallest value of  so that every such coloring of
so that every such coloring of  points of
points of  is good.
is good. It is known that 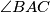 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 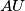 at
at  and
and  , respectively. The lines
, respectively. The lines 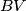 and
and 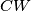 meet at
meet at  .
.
Show that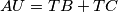 .
.
Alternative formulation:
Four different points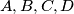 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that:
(a) The perpendicular bisectors of and
and  meet the line
meet the line  at certain points
at certain points  and
and 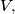 respectively, and that the lines
respectively, and that the lines 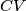 and
and 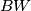 meet at a certain point
meet at a certain point 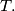
(b) The length of one of the line segments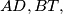 and
and 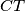 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.
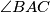 is the smallest angle in the triangle
is the smallest angle in the triangle  . The points
. The points  and
and  divide the circumcircle of the triangle into two arcs. Let
divide the circumcircle of the triangle into two arcs. Let  be an interior point of the arc between
be an interior point of the arc between  and
and  which does not contain
which does not contain  . The perpendicular bisectors of
. The perpendicular bisectors of  and
and  meet the line
meet the line 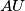 at
at  and
and  , respectively. The lines
, respectively. The lines 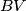 and
and 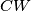 meet at
meet at  .
. Show that
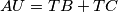 .
. Alternative formulation:
Four different points
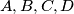 are chosen on a circle
are chosen on a circle  such that the triangle
such that the triangle  is not right-angled. Prove that:
is not right-angled. Prove that: (a) The perpendicular bisectors of
 and
and  meet the line
meet the line  at certain points
at certain points  and
and 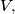 respectively, and that the lines
respectively, and that the lines 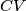 and
and 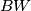 meet at a certain point
meet at a certain point 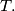
(b) The length of one of the line segments
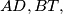 and
and 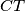 is the sum of the lengths of the other two.
is the sum of the lengths of the other two.  Školjka
Školjka  and
and 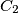 with centers
with centers 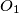 and
and 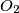 respectively. One of the common tangents to the circles touches
respectively. One of the common tangents to the circles touches 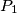 and
and 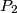 , while the other touches
, while the other touches 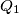 and
and 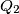 . Let
. Let 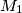 be the midpoint of
be the midpoint of 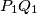 and
and 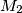 the midpoint of
the midpoint of 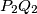 . Prove that
. Prove that 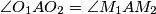 .
.  . Tangents to the circle parallel to the sides of the triangle are contructe. Each of these tangents cuts off a triagnle from
. Tangents to the circle parallel to the sides of the triangle are contructe. Each of these tangents cuts off a triagnle from  . In each of these triangles, a circle is inscribed. Find the sum of the areas of all four inscribed circles (in terms of
. In each of these triangles, a circle is inscribed. Find the sum of the areas of all four inscribed circles (in terms of  at
at  and meets the circumcircle of
and meets the circumcircle of  . From
. From  and
and  respectively. Prove that the quadrilateral
respectively. Prove that the quadrilateral 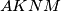 and the triangle
and the triangle  of a circle intersect at a point
of a circle intersect at a point 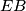 . The tangent line at
. The tangent line at  ,
,  and
and  , respectively. If
, respectively. If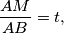
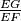 in terms of
in terms of  .
.