Dana je polukružnica nad promjerom

i na njoj točke

i

tako da vrijedi:
a) točka

pripada luku

;
b)
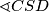
je pravi, pri čemu je

središte dužine

.
Neka je

sjecište pravaca

i

, a

sjecište

i

. Dokažite da je
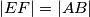
.
%V0
Dana je polukružnica nad promjerom $\overline{AB}$ i na njoj točke $C$ i $D$ tako da vrijedi:
a) točka $C$ pripada luku $AD$;
b) $\sphericalangle CSD$ je pravi, pri čemu je $S$ središte dužine $\overline{AB}$.
Neka je $E$ sjecište pravaca $AC$ i $BD$, a $F$ sjecište $AD$ i $BC$. Dokažite da je $|EF| = |AB|$.