Slični zadaci
Kružnice  i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 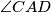 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.
 i
i  sijeku se u točkama
sijeku se u točkama  i
i  . Tangenta kružnice
. Tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  , a tangenta kružnice
, a tangenta kružnice  povučena iz točke
povučena iz točke  siječe kružnicu
siječe kružnicu  u točki
u točki  . Polupravac kroz točku
. Polupravac kroz točku  , koji leži unutar kuta
, koji leži unutar kuta 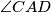 , siječe kružnicu
, siječe kružnicu  u točki
u točki  , kružnicu
, kružnicu  u točki
u točki  i kružnicu opisanu trokutu
i kružnicu opisanu trokutu  u točki
u točki  . Dokaži da je udaljenost točaka
. Dokaži da je udaljenost točaka  i
i  jednaka udaljenosti točaka
jednaka udaljenosti točaka  i
i  .
.  Školjka
Školjka  i na njoj točke
i na njoj točke  ;
;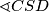 je pravi, pri čemu je
je pravi, pri čemu je  središte dužine
središte dužine  sjecište pravaca
sjecište pravaca  i
i  , a
, a  sjecište
sjecište  . Dokažite da je
. Dokažite da je 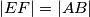 .
.  nalazi se točka
nalazi se točka  dira stranicu
dira stranicu  i produžetke stranica
i produžetke stranica  trokuta
trokuta  ,
,  . Dužine
. Dužine 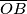 i
i 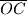 sijeku spojnicu
sijeku spojnicu 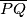 redom u točkama
redom u točkama 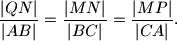
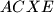 i
i 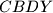 . Dokažite da se pravci
. Dokažite da se pravci  sijeku na visini iz vrha
sijeku na visini iz vrha  i
i  . ako je
. ako je 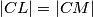 , dokazite da je
, dokazite da je 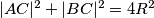 , gdje je
, gdje je  duljina polumjera kruznice opisane trokutu
duljina polumjera kruznice opisane trokutu 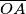 promjer i
promjer i  polumjera
polumjera 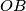 i tangente na
i tangente na  točka na dužini
točka na dužini 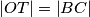 i
i 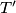 projekcija od
projekcija od 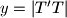 kao funkciju od
kao funkciju od 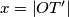 .
.