a) Dokaži da za međusobno različite prirodne brojeve

i

postoji beskonačno mnogo prirodnih brojeva

takvih da su brojevi
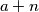
i
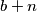
relativno prosti.
b) Postoje li međusobno različiti prirodni brojevi

,

,

i

za koje ne postoji prirodni broj

takav da su brojevi
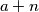
,
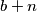
,
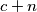
,
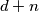
u parovima relativno prosti?
%V0
a) Dokaži da za međusobno različite prirodne brojeve $a$ i $b$ postoji beskonačno mnogo prirodnih brojeva $n$ takvih da su brojevi $a+n$ i $b+n$ relativno prosti.
b) Postoje li međusobno različiti prirodni brojevi $a$, $b$, $c$ i $d$ za koje ne postoji prirodni broj $n$ takav da su brojevi $a+n$, $b+n$, $c+n$, $d+n$ u parovima relativno prosti?