Chords

and

of a circle intersect at a point

inside the circle. Let

be an interior point of the segment
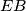
. The tangent line at

to the circle through

,

, and

intersects the lines

and

at

and
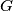
, respectively. If
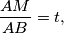
find
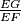
in terms of
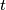
.
%V0
Chords $AB$ and $CD$ of a circle intersect at a point $E$ inside the circle. Let $M$ be an interior point of the segment $EB$. The tangent line at $E$ to the circle through $D$, $E$, and $M$ intersects the lines $BC$ and $AC$ at $F$ and $G$, respectively. If
$$\frac {AM}{AB} = t,$$
find $\frac {EG}{EF}$ in terms of $t$.