We call a set

on the real line
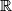
superinvariant if for any stretching

of the set by the transformation taking

to
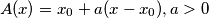
there exists a translation

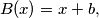
such that the images of

under

and

agree; i.e., for any
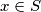
there is a
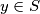
such that
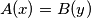
and for any
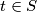
there is a
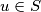
such that
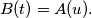
Determine all superinvariant sets.
%V0
We call a set $S$ on the real line $\mathbb{R}$ superinvariant if for any stretching $A$ of the set by the transformation taking $x$ to $A(x) = x_0 + a(x - x_0), a > 0$ there exists a translation $B,$ $B(x) = x+b,$ such that the images of $S$ under $A$ and $B$ agree; i.e., for any $x \in S$ there is a $y \in S$ such that $A(x) = B(y)$ and for any $t \in S$ there is a $u \in S$ such that $B(t) = A(u).$ Determine all superinvariant sets.