Slični zadaci
A convex quadrilateral has equal diagonals. An equilateral triangle is constructed on the outside of each side of the quadrilateral. The centers of the triangles on opposite sides are joined. Show that the two joining lines are perpendicular.
Alternative formulation. Given a convex quadrilateral with congruent diagonals
with congruent diagonals 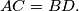 Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Original formulation: Let be a convex quadrilateral such that
be a convex quadrilateral such that 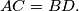 Equilateral triangles are constructed on the sides of the quadrilateral. Let
Equilateral triangles are constructed on the sides of the quadrilateral. Let 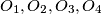 be the centers of the triangles constructed on
be the centers of the triangles constructed on 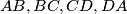 respectively. Show that
respectively. Show that 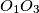 is perpendicular to
is perpendicular to 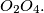
Alternative formulation. Given a convex quadrilateral
 with congruent diagonals
with congruent diagonals 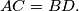 Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other.
Four regular triangles are errected externally on its sides. Prove that the segments joining the centroids of the triangles on the opposite sides are perpendicular to each other. Original formulation: Let
 be a convex quadrilateral such that
be a convex quadrilateral such that 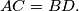 Equilateral triangles are constructed on the sides of the quadrilateral. Let
Equilateral triangles are constructed on the sides of the quadrilateral. Let 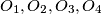 be the centers of the triangles constructed on
be the centers of the triangles constructed on 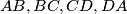 respectively. Show that
respectively. Show that 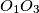 is perpendicular to
is perpendicular to 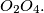
 Školjka
Školjka 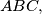 let
let  and
and  be the intersections of the bisectors of
be the intersections of the bisectors of 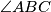 and
and 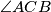 with the sides
with the sides 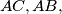 respectively. Determine the angles
respectively. Determine the angles 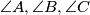 if
if 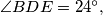
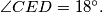
 parallel lines
parallel lines 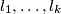 and
and 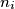 points on the line
points on the line 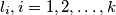 , find the maximum possible number of triangles with vertices at these points.
, find the maximum possible number of triangles with vertices at these points. 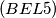 Let
Let  be the centroid of the triangle
be the centroid of the triangle 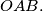
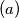 Prove that all conics passing through the points
Prove that all conics passing through the points 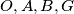 are hyperbolas.
are hyperbolas.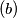 Find the locus of the centers of these hyperbolas.
Find the locus of the centers of these hyperbolas. 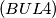 Let
Let  be the point inside the right-angled triangle
be the point inside the right-angled triangle 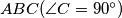 such that
such that 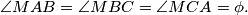 Let
Let 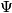 be the acute angle between the medians of
be the acute angle between the medians of  and
and 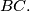 Prove that
Prove that 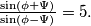
 with points
with points  are in the sides
are in the sides  and
and 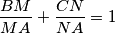 , then prove that the centroid of
, then prove that the centroid of  .
.  Six points
Six points 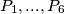 are given in
are given in 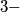 dimensional space such that no four of them lie in the same plane. Each of the line segments
dimensional space such that no four of them lie in the same plane. Each of the line segments 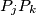 is colored black or white. Prove that there exists one triangle
is colored black or white. Prove that there exists one triangle 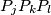 whose edges are of the same color.
whose edges are of the same color.