In the plane let
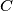
be a circle,
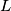
a line tangent to the circle
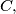
and
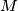
a point on
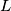
. Find the locus of all points
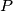
with the following property: there exists two points
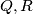
on
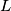
such that
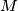
is the midpoint of
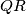
and
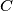
is the inscribed circle of triangle
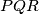
.
%V0
In the plane let $\,C\,$ be a circle, $\,L\,$ a line tangent to the circle $\,C,\,$ and $\,M\,$ a point on $\,L$. Find the locus of all points $\,P\,$ with the following property: there exists two points $\,Q,R\,$ on $\,L\,$ such that $\,M\,$ is the midpoint of $\,QR\,$ and $\,C\,$ is the inscribed circle of triangle $\,PQR$.