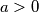
and

,

are integers such that
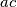
–
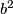
is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let

be the number of pairs of integers
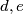
such that
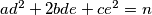
. Show that

is finite and that
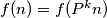
for every positive integer

.
Original Statement:
Let

be given integers
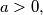
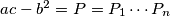
where
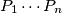
are (distinct) prime numbers. Let
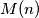
denote the number of pairs of integers
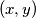
for which
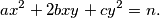
Prove that
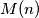
is finite and
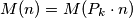
for every integer
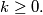
Note that the "

" in
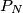
and the "

" in
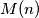
do not have to be the same.
%V0
$a > 0$ and $b$, $c$ are integers such that $ac$ – $b^2$ is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let $f(n)$ be the number of pairs of integers $d, e$ such that $ad^2 + 2bde + ce^2= n$. Show that$f(n)$ is finite and that $f(n) = f(P^{k}n)$ for every positive integer $k$.
Original Statement:
Let $a,b,c$ be given integers $a > 0,$ $ac-b^2 = P = P_1 \cdots P_n$ where $P_1 \cdots P_n$ are (distinct) prime numbers. Let $M(n)$ denote the number of pairs of integers $(x,y)$ for which $$ax^2 + 2bxy + cy^2 = n.$$ Prove that $M(n)$ is finite and $M(n) = M(P_k \cdot n)$ for every integer $k \geq 0.$ Note that the "$n$" in $P_N$ and the "$n$" in $M(n)$ do not have to be the same.
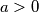 and
and  ,
,  are integers such that
are integers such that 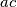 –
– 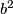 is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let
is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let  be the number of pairs of integers
be the number of pairs of integers 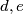 such that
such that 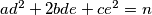 . Show that
. Show that is finite and that
is finite and that 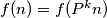 for every positive integer
for every positive integer  .
.  be given integers
be given integers 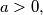
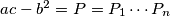 where
where 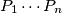 are (distinct) prime numbers. Let
are (distinct) prime numbers. Let 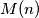 denote the number of pairs of integers
denote the number of pairs of integers 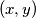 for which
for which 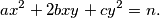 Prove that
Prove that 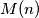 is finite and
is finite and 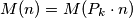 for every integer
for every integer 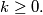 Note that the "
Note that the " " in
" in 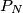 and the "
and the " " in
" in 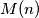 do not have to be the same.
do not have to be the same.  Školjka
Školjka