Let
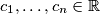
with

such that
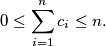
Show that we can find integers
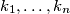
such that
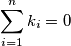
and
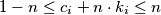
for every
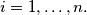
Another formulation:Let
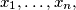
with

be real numbers such that
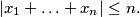
Show that there exist integers
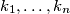
such that
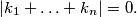
and
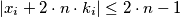
for every
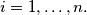
In order to prove this, denote
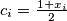
for
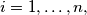
etc.
%V0
Let $c_1, \ldots, c_n \in \mathbb{R}$ with $n \geq 2$ such that $$0 \leq \sum^n_{i=1} c_i \leq n.$$ Show that we can find integers $k_1, \ldots, k_n$ such that $$\sum^n_{i=1} k_i = 0$$ and $$1-n \leq c_i + n \cdot k_i \leq n$$ for every $i = 1, \ldots, n.$
Another formulation:Let $x_1, \ldots, x_n,$ with $n \geq 2$ be real numbers such that $$|x_1 + \ldots + x_n| \leq n.$$ Show that there exist integers $k_1, \ldots, k_n$ such that $$|k_1 + \ldots + k_n| = 0.$$ and $$|x_i + 2 \cdot n \cdot k_i| \leq 2 \cdot n -1$$ for every $i = 1, \ldots, n.$ In order to prove this, denote $c_i = \frac{1+x_i}{2}$ for $i = 1, \ldots, n,$ etc.