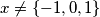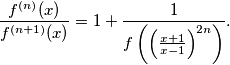Slični zadaci
 and
and  ,
,  are integers such that
are integers such that  –
– 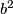 is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let
is a square-free positive integer P. For example P could be 3*5, but not 3^2*5. Let  be the number of pairs of integers
be the number of pairs of integers 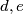 such that
such that 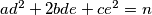 . Show that
. Show that is finite and that
is finite and that 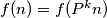 for every positive integer
for every positive integer  .
. Original Statement:
Let
 be given integers
be given integers 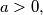
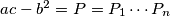 where
where 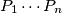 are (distinct) prime numbers. Let
are (distinct) prime numbers. Let 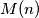 denote the number of pairs of integers
denote the number of pairs of integers 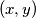 for which
for which 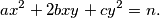 Prove that
Prove that 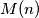 is finite and
is finite and 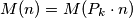 for every integer
for every integer 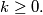 Note that the "
Note that the " " in
" in 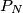 and the "
and the " " in
" in 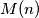 do not have to be the same.
do not have to be the same.  Školjka
Školjka 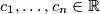 with
with  such that
such that 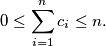 Show that we can find integers
Show that we can find integers 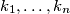 such that
such that 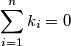 and
and 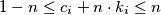 for every
for every 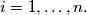
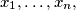 with
with 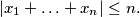 Show that there exist integers
Show that there exist integers 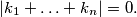 and
and 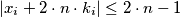 for every
for every 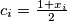 for
for 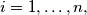 etc.
etc. 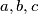 are three positive real numbers such that
are three positive real numbers such that 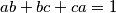 , prove that
, prove that ![\sqrt[3]{ \frac{1}{a} + 6b} + \sqrt[3]{\frac{1}{b} + 6c} + \sqrt[3]{\frac{1}{c} + 6a } \leq \frac{1}{abc}.](/media/m/b/8/1/b8152e5174c814f5f157b14f7eb88b60.png)
 be a non-empty set of positive integers. Suppose that there are positive integers
be a non-empty set of positive integers. Suppose that there are positive integers 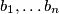 and
and 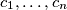 such that
such that  the set
the set 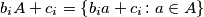 is a subset of
is a subset of 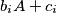 and
and 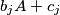 are disjoint whenever
are disjoint whenever 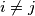
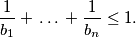
![a=\root3\of n\kern1.5pt,\qquad b={1\over a-[a]}\kern1pt,\qquad c={1\over b-[b]}\kern1.5pt,](/media/m/8/2/d/82d50c7f89d4ecc16f6afad9981c6d07.png)
![[x]](/media/m/6/a/4/6a47dfb91475b9d5490dbb3a666604a3.png) denotes the integer part of
denotes the integer part of  . Prove that there are infinitely many such integers
. Prove that there are infinitely many such integers 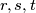 , not all zero, such that
, not all zero, such that 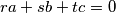 .
. 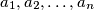 such that
such that 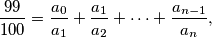
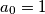 and
and 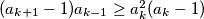 for
for 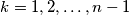 .
. 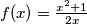 for
for 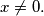 Define
Define 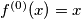 and
and 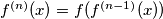 for all positive integers
for all positive integers