Slični zadaci
A finite number of coins are placed on an infinite row of squares. A sequence of moves is performed as follows: at each stage a square containing more than one coin is chosen. Two coins are taken from this square; one of them is placed on the square immediately to the left while the other is placed on the square immediately to the right of the chosen square. The sequence terminates if at some point there is at most one coin on each square. Given some initial configuration, show that any legal sequence of moves will terminate after the same number of steps and with the same final configuration.
For a positive integer  define a sequence of zeros and ones to be balanced if it contains
define a sequence of zeros and ones to be balanced if it contains  zeros and
zeros and  ones. Two balanced sequences
ones. Two balanced sequences  and
and  are neighbors if you can move one of the
are neighbors if you can move one of the  symbols of
symbols of  to another position to form
to another position to form  . For instance, when
. For instance, when 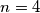 , the balanced sequences
, the balanced sequences 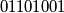 and
and 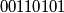 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set
are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set  of at most
of at most 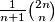 balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in
balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in  .
.
 define a sequence of zeros and ones to be balanced if it contains
define a sequence of zeros and ones to be balanced if it contains  zeros and
zeros and  ones. Two balanced sequences
ones. Two balanced sequences  and
and  are neighbors if you can move one of the
are neighbors if you can move one of the  symbols of
symbols of  to another position to form
to another position to form  . For instance, when
. For instance, when 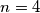 , the balanced sequences
, the balanced sequences 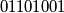 and
and 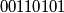 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set
are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set  of at most
of at most 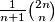 balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in
balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in  .
. There are  markers, each with one side white and the other side black. In the beginning, these
markers, each with one side white and the other side black. In the beginning, these  markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if
markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if 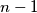 is not divisible by
is not divisible by  .
.
 markers, each with one side white and the other side black. In the beginning, these
markers, each with one side white and the other side black. In the beginning, these  markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if
markers are aligned in a row so that their white sides are all up. In each step, if possible, we choose a marker whose white side is up (but not one of the outermost markers), remove it, and reverse the closest marker to the left of it and also reverse the closest marker to the right of it. Prove that, by a finite sequence of such steps, one can achieve a state with only two markers remaining if and only if 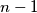 is not divisible by
is not divisible by  .
. Five identical empty buckets of  -liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighbouring buckets, empties them to the river and puts them back. Then the next round begins. The Stepmother goal's is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?
-liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighbouring buckets, empties them to the river and puts them back. Then the next round begins. The Stepmother goal's is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?
Proposed by Gerhard Woeginger, Netherlands
 -liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighbouring buckets, empties them to the river and puts them back. Then the next round begins. The Stepmother goal's is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?
-liter capacity stand at the vertices of a regular pentagon. Cinderella and her wicked Stepmother go through a sequence of rounds: At the beginning of every round, the Stepmother takes one liter of water from the nearby river and distributes it arbitrarily over the five buckets. Then Cinderella chooses a pair of neighbouring buckets, empties them to the river and puts them back. Then the next round begins. The Stepmother goal's is to make one of these buckets overflow. Cinderella's goal is to prevent this. Can the wicked Stepmother enforce a bucket overflow?Proposed by Gerhard Woeginger, Netherlands
 Školjka
Školjka 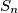 be the number of sequences
be the number of sequences 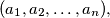 where
where 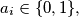 in which no six consecutive blocks are equal. Prove that
in which no six consecutive blocks are equal. Prove that 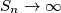 when
when 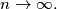
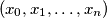 such that for every
such that for every  ,
, 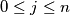 ,
, 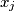 equals the number of times
equals the number of times 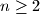 , let
, let  ,
, 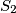 ,
,  ,
, 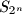 be
be 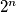 subsets of
subsets of 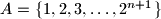 that satisfy the following property: There do not exist indices
that satisfy the following property: There do not exist indices 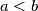 and elements
and elements  ,
,  ,
, 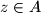 with
with 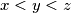 and
and 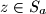 , and
, and 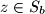 . Prove that at least one of the sets
. Prove that at least one of the sets 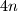 elements.
elements.