Let  ,
,  ,
,  ,
,  be four points in the plane, with
be four points in the plane, with  and
and  on the same side of the line
on the same side of the line  , such that
, such that 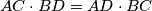 and
and 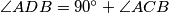 . Find the ratio
. Find the ratio
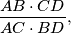
and prove that the circumcircles of the triangles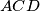 and
and  are orthogonal. (Intersecting circles are said to be orthogonal if at either common point their tangents are perpendicuar. Thus, proving that the circumcircles of the triangles
are orthogonal. (Intersecting circles are said to be orthogonal if at either common point their tangents are perpendicuar. Thus, proving that the circumcircles of the triangles 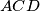 and
and  are orthogonal is equivalent to proving that the tangents to the circumcircles of the triangles
are orthogonal is equivalent to proving that the tangents to the circumcircles of the triangles 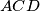 and
and  at the point
at the point  are perpendicular.)
are perpendicular.)
 ,
,  ,
,  ,
,  be four points in the plane, with
be four points in the plane, with  and
and  on the same side of the line
on the same side of the line  , such that
, such that 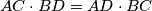 and
and 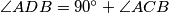 . Find the ratio
. Find the ratio 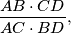
and prove that the circumcircles of the triangles
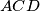 and
and  are orthogonal. (Intersecting circles are said to be orthogonal if at either common point their tangents are perpendicuar. Thus, proving that the circumcircles of the triangles
are orthogonal. (Intersecting circles are said to be orthogonal if at either common point their tangents are perpendicuar. Thus, proving that the circumcircles of the triangles 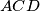 and
and  are orthogonal is equivalent to proving that the tangents to the circumcircles of the triangles
are orthogonal is equivalent to proving that the tangents to the circumcircles of the triangles 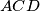 and
and  at the point
at the point  are perpendicular.)
are perpendicular.)  Školjka
Školjka