IMO Shortlist 2008 problem G7
Kvaliteta:
Avg: 4,0Težina:
Avg: 8,5 Let  be a convex quadrilateral with
be a convex quadrilateral with 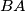 different from
different from  . Denote the incircles of triangles
. Denote the incircles of triangles  and
and 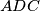 by
by 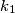 and
and 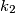 respectively. Suppose that there exists a circle
respectively. Suppose that there exists a circle  tangent to ray
tangent to ray 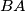 beyond
beyond  and to the ray
and to the ray  beyond
beyond  , which is also tangent to the lines
, which is also tangent to the lines  and
and  .
.
Prove that the common external tangents to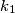 and
and 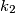 intersects on
intersects on  .
.
Author: Vladimir Shmarov, Russia
 be a convex quadrilateral with
be a convex quadrilateral with 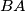 different from
different from  . Denote the incircles of triangles
. Denote the incircles of triangles  and
and 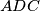 by
by 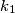 and
and 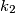 respectively. Suppose that there exists a circle
respectively. Suppose that there exists a circle  tangent to ray
tangent to ray 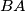 beyond
beyond  and to the ray
and to the ray  beyond
beyond  , which is also tangent to the lines
, which is also tangent to the lines  and
and  .
. Prove that the common external tangents to
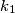 and
and 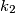 intersects on
intersects on  .
. Author: Vladimir Shmarov, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2008
 Školjka
Školjka 
