Slični zadaci
A circle  bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively).
Show that are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points.
Original Statement:
A circle is said to cut a circle
is said to cut a circle 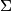 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 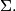
Let be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 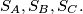
 bisects a circle
bisects a circle  if it cuts
if it cuts  at opposite ends of a diameter.
at opposite ends of a diameter.  ,
,  ,
, are circles with distinct centers
are circles with distinct centers  (respectively).
(respectively). Show that
 are collinear iff there is no unique circle
are collinear iff there is no unique circle  which bisects each of
which bisects each of  ,
,  ,
, . Show that if there is more than one circle
. Show that if there is more than one circle  which bisects each of
which bisects each of  ,
,  ,
, , then all such circles pass through two fixed points. Find these points.
, then all such circles pass through two fixed points. Find these points. Original Statement:
A circle
 is said to cut a circle
is said to cut a circle 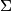 diametrically if and only if their common chord is a diameter of
diametrically if and only if their common chord is a diameter of 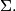
Let
 be three circles with distinct centres
be three circles with distinct centres  respectively. Prove that
respectively. Prove that  are collinear if and only if there is no unique circle
are collinear if and only if there is no unique circle  which cuts each of
which cuts each of  diametrically. Prove further that if there exists more than one circle
diametrically. Prove further that if there exists more than one circle  which cuts each
which cuts each  diametrically, then all such circles
diametrically, then all such circles  pass through two fixed points. Locate these points in relation to the circles
pass through two fixed points. Locate these points in relation to the circles 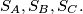
Given trapezoid  with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 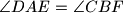 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 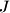 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 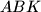 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 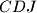 .
.
Proposed by Charles Leytem, Luxembourg
 with parallel sides
with parallel sides  and
and  , assume that there exist points
, assume that there exist points  on line
on line  outside segment
outside segment  , and
, and  inside segment
inside segment  such that
such that 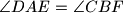 . Denote by
. Denote by  the point of intersection of
the point of intersection of  and
and  , and by
, and by 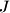 the point of intersection of
the point of intersection of  and
and  . Let
. Let  be the midpoint of segment
be the midpoint of segment  , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 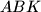 if and only if
if and only if  belongs to the circumcircle of
belongs to the circumcircle of 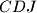 .
. Proposed by Charles Leytem, Luxembourg
 Školjka
Školjka 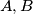 and
and  be non-collinear points. Prove that there is a unique point
be non-collinear points. Prove that there is a unique point  in the plane of
in the plane of  such that
such that 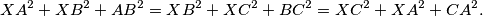
 points on the boundary of the circle ?
points on the boundary of the circle ?  be a positive integer. Show that there are infinitely many perfect squares of the form
be a positive integer. Show that there are infinitely many perfect squares of the form 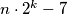 where
where 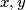 and
and  in positive integer:
in positive integer: 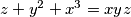 and
and 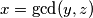 .
. 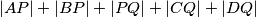 , gdje su
, gdje su  i
i  točke unutar jediničnog kvadrata
točke unutar jediničnog kvadrata