Neka je
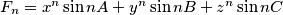
, gdje su
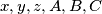
realni brojevi takvi da je
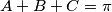
. Ako je
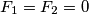
, dokažite da je
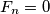
za svaki prirodni broj

.
%V0
Neka je $F_n=x^n \sin nA + y^n \sin nB + z^n \sin nC$, gdje su $x, y, z, A, B, C$ realni brojevi takvi da je $A+B+C=\pi$. Ako je $F_1=F_2=0$, dokažite da je $F_n=0$ za svaki prirodni broj $n$.