Let

be an acute triangle with circumcenter

and circumradius

.
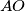
meets the circumcircle of
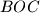
at
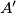
,
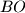
meets the circumcircle of
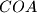
at
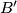
and
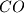
meets the circumcircle of
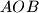
at
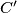
. Prove that
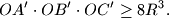
Sorry if this has been posted before since this is a very classical problem, but I failed to find it with the search-function.
%V0
Let $ABC$ be an acute triangle with circumcenter $O$ and circumradius $R$. $AO$ meets the circumcircle of $BOC$ at $A'$, $BO$ meets the circumcircle of $COA$ at $B'$ and $CO$ meets the circumcircle of $AOB$ at $C'$. Prove that $$OA'\cdot OB'\cdot OC'\geq 8R^{3}.$$ Sorry if this has been posted before since this is a very classical problem, but I failed to find it with the search-function.