IMO Shortlist 2004 problem G7
Dodao/la:
arhiva2. travnja 2012. For a given triangle

, let

be a variable point on the line

such that

lies between

and

and the incircles of the triangles
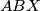
and
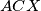
intersect at two distinct points

and
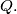
Prove that the line

passes through a point independent of

.
comment
An extension by Darij Grinberg can be found here.
%V0
For a given triangle $ABC$, let $X$ be a variable point on the line $BC$ such that $C$ lies between $B$ and $X$ and the incircles of the triangles $ABX$ and $ACX$ intersect at two distinct points $P$ and $Q.$ Prove that the line $PQ$ passes through a point independent of $X$.
comment
An extension by Darij Grinberg can be found here.
Izvor: Međunarodna matematička olimpijada, shortlist 2004