The positive integers

and

are such that the numbers
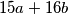
and
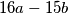
are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?
%V0
The positive integers $a$ and $b$ are such that the numbers $15a + 16b$ and $16a - 15b$ are both squares of positive integers. What is the least possible value that can be taken on by the smaller of these two squares?