In town  there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 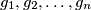 and
and 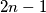 boys
boys 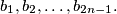 The girl
The girl 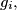
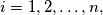 knows the boys
knows the boys 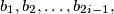 and no others. For all
and no others. For all 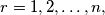 denote by
denote by 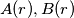 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 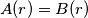 for each
for each 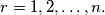
 there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 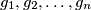 and
and 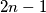 boys
boys 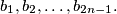 The girl
The girl 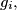
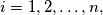 knows the boys
knows the boys 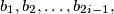 and no others. For all
and no others. For all 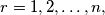 denote by
denote by 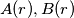 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 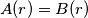 for each
for each 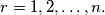
 Školjka
Školjka 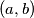 of positive integers that satisfy the equation:
of positive integers that satisfy the equation: 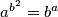 .
.  of an acute-angled triangle
of an acute-angled triangle  meet the opposite sides at
meet the opposite sides at  respectively. The line through
respectively. The line through  parallel to
parallel to  meets the lines
meets the lines  and
and  at
at  and
and  respectively. The line
respectively. The line  at
at 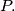 Prove that the circumcircle of the triangle
Prove that the circumcircle of the triangle 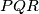 passes through the midpoint of
passes through the midpoint of 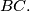
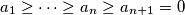 be real numbers. Show that
be real numbers. Show that 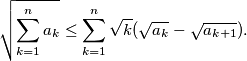
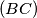 . The line
. The line  meets the circumcircle again at
meets the circumcircle again at  .
.  is the foot of the perpendicular from
is the foot of the perpendicular from  is a tangent to the circle on diameter
is a tangent to the circle on diameter 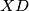 if and only if
if and only if 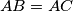 .
. 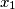 ,
, 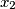 ,
,  ,
, 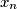 be real numbers satisfying the conditions:
be real numbers satisfying the conditions: 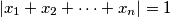 and
and 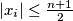 , for
, for 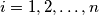
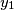 ,
, 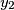 ,
, 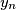 of
of 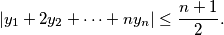
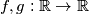 such that
such that 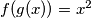 and
and 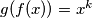 for all real numbers
for all real numbers 
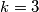 ?
? 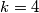 ?
?