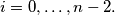Slični zadaci
In town  there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 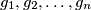 and
and 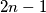 boys
boys 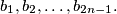 The girl
The girl 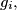
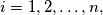 knows the boys
knows the boys 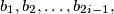 and no others. For all
and no others. For all 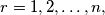 denote by
denote by 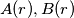 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 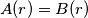 for each
for each 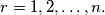
 there are
there are  girls and
girls and  boys, and each girl knows each boy. In town
boys, and each girl knows each boy. In town  there are
there are  girls
girls 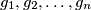 and
and 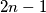 boys
boys 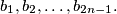 The girl
The girl 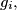
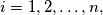 knows the boys
knows the boys 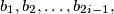 and no others. For all
and no others. For all 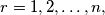 denote by
denote by 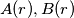 the number of different ways in which
the number of different ways in which  girls from town
girls from town  respectively town
respectively town  can dance with
can dance with  boys from their own town, forming
boys from their own town, forming  pairs, each girl with a boy she knows. Prove that
pairs, each girl with a boy she knows. Prove that 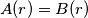 for each
for each 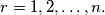
 Školjka
Školjka 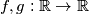 such that
such that 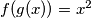 and
and 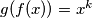 for all real numbers
for all real numbers 
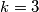 ?
? 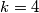 ?
? 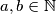 with
with 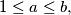 and
and ![M = \left[\frac {a + b}{2} \right].](/media/m/7/2/c/72cf1d082062d5caeb7a120b0b87a896.png) Define a function
Define a function 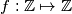 by
by 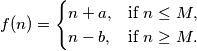
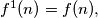
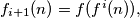
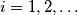 Find the smallest natural number
Find the smallest natural number  such that
such that 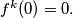
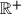 be the set of all non-negative real numbers. Given two positive real numbers
be the set of all non-negative real numbers. Given two positive real numbers  and
and 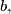 suppose that a mapping
suppose that a mapping 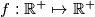 satisfies the functional equation:
satisfies the functional equation: 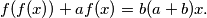
 be a polynomial with real coefficients such that
be a polynomial with real coefficients such that 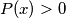 for all
for all 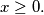 Prove that there exists a positive integer n such that
Prove that there exists a positive integer n such that 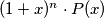 is a polynomial with nonnegative coefficients.
is a polynomial with nonnegative coefficients. 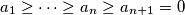 be real numbers. Show that
be real numbers. Show that 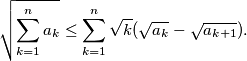
 determine the minimum value that the sum
determine the minimum value that the sum 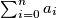 can take for nonnegative numbers
can take for nonnegative numbers 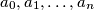 satisfying the condition
satisfying the condition 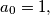
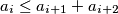 for
for