Let
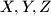
be the midpoints of the small arcs
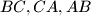
respectively (arcs of the circumcircle of

).

is an arbitrary point on

, and the parallels through

to the internal bisectors of
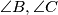
cut the external bisectors of
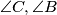
in
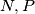
respectively. Show that
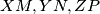
concur.
%V0
Let $X,Y,Z$ be the midpoints of the small arcs $BC,CA,AB$ respectively (arcs of the circumcircle of $ABC$). $M$ is an arbitrary point on $BC$, and the parallels through $M$ to the internal bisectors of $\angle B,\angle C$ cut the external bisectors of $\angle C,\angle B$ in $N,P$ respectively. Show that $XM,YN,ZP$ concur.