Neka su  i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:
a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je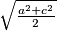 (kvadratna sredina).
(kvadratna sredina).
b) Duljina spojnice polovišta krakova jednaka je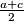 (aritmetička sredina).
(aritmetička sredina).
c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je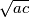 (geometrijska sredina).
(geometrijska sredina).
d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je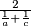 (harmonijska sredina).
(harmonijska sredina).
 i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je
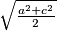 (kvadratna sredina).
(kvadratna sredina).b) Duljina spojnice polovišta krakova jednaka je
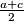 (aritmetička sredina).
(aritmetička sredina).c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je
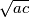 (geometrijska sredina).
(geometrijska sredina).d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je
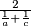 (harmonijska sredina).
(harmonijska sredina).  Školjka
Školjka  , a kutovi uz jednu osnovicu su
, a kutovi uz jednu osnovicu su 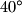 i
i 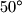 . Odredite duljine osnovica ako je udaljenost njihovih polovišta jednaka
. Odredite duljine osnovica ako je udaljenost njihovih polovišta jednaka  .
.  i
i  trokuta
trokuta  međusobno okomite ako i samo ako za duljine stranica vrijedi jednakost
međusobno okomite ako i samo ako za duljine stranica vrijedi jednakost 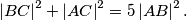
 i
i  je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi
je duljina polumjera opisane mu kružnice. Odredite kutove trokuta ako vrijedi 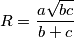 .
.  i
i  sa zajedničkim početkom
sa zajedničkim početkom  dane su točke
dane su točke  (na
(na  (na
(na  paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 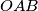 , dokažite da je pravac
, dokažite da je pravac  paralelan s težišnicom trokuta
paralelan s težišnicom trokuta 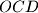 .
.