Let

be a positive integer. Consider
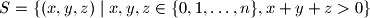
as a set of
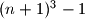
points in the three-dimensional space. Determine the smallest possible number of planes, the union of which contains

but does not include
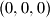
.
Author: Gerhard Wöginger, Netherlands
%V0
Let $n$ be a positive integer. Consider
$$S = \left\{ (x,y,z) \mid x,y,z \in \{ 0, 1, \ldots, n\}, x + y + z > 0 \right \}$$
as a set of $(n + 1)^{3} - 1$ points in the three-dimensional space. Determine the smallest possible number of planes, the union of which contains $S$ but does not include $(0,0,0)$.
Author: Gerhard Wöginger, Netherlands