Slični zadaci
In the coordinate plane consider the set  of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 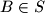 will be called
will be called  -friends if there is a point
-friends if there is a point 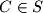 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 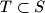 will be called
will be called  -clique if every two points in
-clique if every two points in  are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements.
Proposed by Jorge Tipe, Peru
 of all points with integer coordinates. For a positive integer
of all points with integer coordinates. For a positive integer  , two distinct points
, two distinct points  ,
, 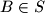 will be called
will be called  -friends if there is a point
-friends if there is a point 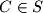 such that the area of the triangle
such that the area of the triangle  is equal to
is equal to  . A set
. A set 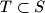 will be called
will be called  -clique if every two points in
-clique if every two points in  are
are  -friends. Find the least positive integer
-friends. Find the least positive integer  for which there exits a
for which there exits a  -clique with more than 200 elements.
-clique with more than 200 elements. Proposed by Jorge Tipe, Peru
 Školjka
Školjka 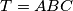 we take the point
we take the point  on the side
on the side 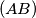 such that
such that 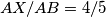 , the point
, the point  on the segment
on the segment 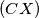 such that
such that 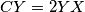 and, if possible, the point
and, if possible, the point  on the ray (
on the ray ( such that
such that 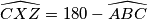 . We denote by
. We denote by 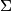 the set of all triangles
the set of all triangles 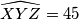 . Prove that all triangles from
. Prove that all triangles from 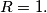 Let
Let  be the inradius of
be the inradius of  be the inradius of the orthic triangle
be the inradius of the orthic triangle 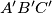 of triangle
of triangle  Prove that
Prove that 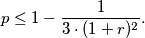
 and
and  be points on the side
be points on the side  such that
such that 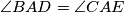 . If
. If  and
and  are, respectively, the points of tangency of the incircles of the triangles
are, respectively, the points of tangency of the incircles of the triangles 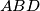 and
and 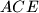 with the line
with the line 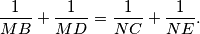
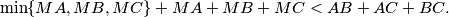
 its incircle and
its incircle and 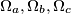 three circles orthogonal to
three circles orthogonal to 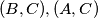 and
and 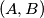 respectively. The circles
respectively. The circles 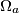 and
and 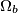 meet again in
meet again in 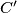 ; in the same way we obtain the points
; in the same way we obtain the points 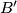 and
and 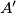 . Prove that the radius of the circumcircle of
. Prove that the radius of the circumcircle of  and
and 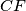 are altitudes. Two circles passing through the point
are altitudes. Two circles passing through the point  anf
anf  and tangent to the line
and tangent to the line  and
and  so that
so that  lies between
lies between  and
and 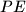 and
and 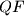 intersect on the circumcircle of triangle
intersect on the circumcircle of triangle 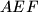 .
.