IMO Shortlist 1999 problem G4
Dodao/la:
arhiva2. travnja 2012. For a triangle
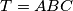
we take the point

on the side
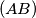
such that
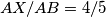
, the point

on the segment
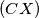
such that
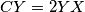
and, if possible, the point

on the ray (

such that
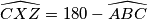
. We denote by
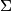
the set of all triangles

for which
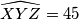
. Prove that all triangles from
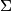
are similar and find the measure of their smallest angle.
%V0
For a triangle $T = ABC$ we take the point $X$ on the side $(AB)$ such that $AX/AB=4/5$, the point $Y$ on the segment $(CX)$ such that $CY = 2YX$ and, if possible, the point $Z$ on the ray ($CA$ such that $\widehat{CXZ} = 180 - \widehat{ABC}$. We denote by $\Sigma$ the set of all triangles $T$ for which
$\widehat{XYZ} = 45$. Prove that all triangles from $\Sigma$ are similar and find the measure of their smallest angle.
Izvor: Međunarodna matematička olimpijada, shortlist 1999