Let

be a triangle,

its incircle and
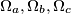
three circles orthogonal to

passing through
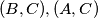
and
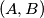
respectively. The circles
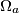
and
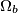
meet again in
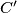
; in the same way we obtain the points
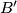
and
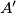
. Prove that the radius of the circumcircle of
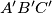
is half the radius of

.
%V0
Let $ABC$ be a triangle, $\Omega$ its incircle and $\Omega_{a}, \Omega_{b}, \Omega_{c}$ three circles orthogonal to $\Omega$ passing through $(B,C),(A,C)$ and $(A,B)$ respectively. The circles $\Omega_{a}$ and $\Omega_{b}$ meet again in $C'$; in the same way we obtain the points $B'$ and $A'$. Prove that the radius of the circumcircle of $A'B'C'$ is half the radius of $\Omega$.