For a polynomial  of degree 2000 with distinct real coefficients let
of degree 2000 with distinct real coefficients let 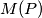 be the set of all polynomials that can be produced from
be the set of all polynomials that can be produced from  by permutation of its coefficients. A polynomial
by permutation of its coefficients. A polynomial  will be called
will be called  -independent if
-independent if 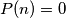 and we can get from any
and we can get from any 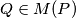 a polynomial
a polynomial 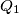 such that
such that 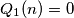 by interchanging at most one pair of coefficients of
by interchanging at most one pair of coefficients of 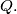 Find all integers
Find all integers  for which
for which  -independent polynomials exist.
-independent polynomials exist.
 of degree 2000 with distinct real coefficients let
of degree 2000 with distinct real coefficients let 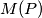 be the set of all polynomials that can be produced from
be the set of all polynomials that can be produced from  by permutation of its coefficients. A polynomial
by permutation of its coefficients. A polynomial  will be called
will be called  -independent if
-independent if 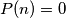 and we can get from any
and we can get from any 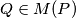 a polynomial
a polynomial 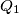 such that
such that 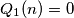 by interchanging at most one pair of coefficients of
by interchanging at most one pair of coefficients of 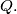 Find all integers
Find all integers  for which
for which  -independent polynomials exist.
-independent polynomials exist.  Školjka
Školjka