Slični zadaci
Each positive integer  is subjected to the following procedure, yielding the number
is subjected to the following procedure, yielding the number 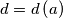 :
:
(a) The last digit of is moved to the first position. The resulting number is called
is moved to the first position. The resulting number is called  .
.
(b) The number is squared. The resulting number is called
is squared. The resulting number is called  .
.
(c) The first digit of is moved to the last position. The resulting number is called
is moved to the last position. The resulting number is called  .
.
(All numbers are considered in the decimal system.) For instance,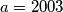 gives
gives 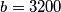 ,
, 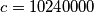 and
and 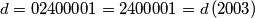 .
.
Find all integers a such that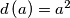 .
.
 is subjected to the following procedure, yielding the number
is subjected to the following procedure, yielding the number 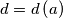 :
: (a) The last digit of
 is moved to the first position. The resulting number is called
is moved to the first position. The resulting number is called  .
. (b) The number
 is squared. The resulting number is called
is squared. The resulting number is called  .
. (c) The first digit of
 is moved to the last position. The resulting number is called
is moved to the last position. The resulting number is called  .
. (All numbers are considered in the decimal system.) For instance,
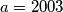 gives
gives 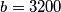 ,
, 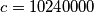 and
and 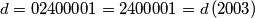 .
. Find all integers a such that
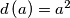 .
.  Školjka
Školjka 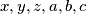 cijeli brojevi za koje vrijedi:
cijeli brojevi za koje vrijedi: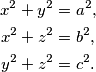 Dokažite da je broj
Dokažite da je broj 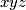 djeljiv s
djeljiv s
 ,
,
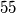 .
. 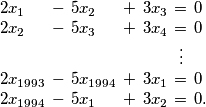
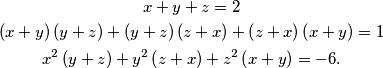
 jednadžbe:
jednadžbe: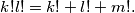
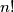 označava umnožak prirodnih brojeva od
označava umnožak prirodnih brojeva od  do
do  .)
.) 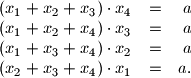
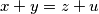 ,
, 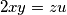 . Find the greatest value of the real constant
. Find the greatest value of the real constant  such that
such that 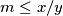 for any positive integer solution
for any positive integer solution 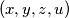 of the system, with
of the system, with 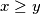 .
.