Let
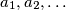
be an infinite sequence of real numbers, for which there exists a real number
with
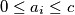
for all
, such that
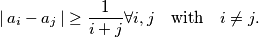
Prove that
.
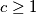
%V0
Let $a_1,a_2,\ldots$ be an infinite sequence of real numbers, for which there exists a real number $c$ with $0\leq a_i\leq c$ for all $i$, such that
$$\left|\,a_i-a_j\,\right|\geq{1\over i+j}{\rm \forall}i,j \quad \textnormal{with} \quad i\ne j.$$
Prove that $c\geq1$.
Školjka