Let
be a cubic polynomial given by
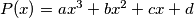
, where
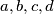
are integers and
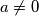
. Suppose that
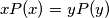
for infinitely many pairs
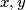
of integers with
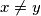
. Prove that the equation
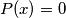
has an integer root.
%V0
Let $P$ be a cubic polynomial given by $P(x)=ax^3+bx^2+cx+d$, where $a,b,c,d$ are integers and $a\ne0$. Suppose that $xP(x)=yP(y)$ for infinitely many pairs $x,y$ of integers with $x\ne y$. Prove that the equation $P(x)=0$ has an integer root.
Školjka