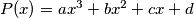
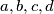
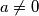
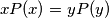
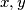
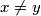
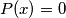
Let be a cubic polynomial given by , where are integers and . Suppose that for infinitely many pairs of integers with . Prove that the equation has an integer root.
%V0
Let $P$ be a cubic polynomial given by $P(x)=ax^3+bx^2+cx+d$, where $a,b,c,d$ are integers and $a\ne0$. Suppose that $xP(x)=yP(y)$ for infinitely many pairs $x,y$ of integers with $x\ne y$. Prove that the equation $P(x)=0$ has an integer root.
Izvor: Međunarodna matematička olimpijada, shortlist 2002
Školjka 
be a cubic polynomial given by 
, where 
are integers and 
. Suppose that 
for infinitely many pairs 
of integers with 
. Prove that the equation 
has an integer root.