Let  be a point on a circle
be a point on a circle  , and let
, and let  be a point distinct from
be a point distinct from  on the tangent at
on the tangent at  to
to  . Let
. Let  be a point not on
be a point not on  such that the line segment
such that the line segment  meets
meets  at two distinct points. Let
at two distinct points. Let 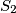 be the circle touching
be the circle touching  at
at  and touching
and touching  at a point
at a point  on the opposite side of
on the opposite side of  from
from  . Prove that the circumcentre of triangle
. Prove that the circumcentre of triangle  lies on the circumcircle of triangle
lies on the circumcircle of triangle  .
.
 be a point on a circle
be a point on a circle  , and let
, and let  be a point distinct from
be a point distinct from  on the tangent at
on the tangent at  to
to  . Let
. Let  be a point not on
be a point not on  such that the line segment
such that the line segment  meets
meets  at two distinct points. Let
at two distinct points. Let 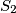 be the circle touching
be the circle touching  at
at  and touching
and touching  at a point
at a point  on the opposite side of
on the opposite side of  from
from  . Prove that the circumcentre of triangle
. Prove that the circumcentre of triangle  lies on the circumcircle of triangle
lies on the circumcircle of triangle  .
.  Školjka
Školjka