Slični zadaci
Let  be a point on a circle
be a point on a circle  , and let
, and let  be a point distinct from
be a point distinct from  on the tangent at
on the tangent at  to
to  . Let
. Let  be a point not on
be a point not on  such that the line segment
such that the line segment  meets
meets  at two distinct points. Let
at two distinct points. Let 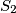 be the circle touching
be the circle touching  at
at  and touching
and touching  at a point
at a point  on the opposite side of
on the opposite side of  from
from  . Prove that the circumcentre of triangle
. Prove that the circumcentre of triangle  lies on the circumcircle of triangle
lies on the circumcircle of triangle  .
.
 be a point on a circle
be a point on a circle  , and let
, and let  be a point distinct from
be a point distinct from  on the tangent at
on the tangent at  to
to  . Let
. Let  be a point not on
be a point not on  such that the line segment
such that the line segment  meets
meets  at two distinct points. Let
at two distinct points. Let 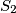 be the circle touching
be the circle touching  at
at  and touching
and touching  at a point
at a point  on the opposite side of
on the opposite side of  from
from  . Prove that the circumcentre of triangle
. Prove that the circumcentre of triangle  lies on the circumcircle of triangle
lies on the circumcircle of triangle  .
.  Školjka
Školjka  and
and  . Distinct points
. Distinct points  and
and  (not at
(not at 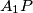 and
and 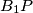 meet
meet  and
and  respectively, and the lines
respectively, and the lines 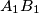 and
and 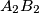 meet at
meet at 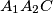 all lie on one fixed circle.
all lie on one fixed circle.  be points on the side
be points on the side  such that
such that 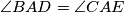 . If
. If  and
and  are, respectively, the points of tangency of the incircles of the triangles
are, respectively, the points of tangency of the incircles of the triangles 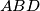 and
and 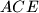 with the line
with the line 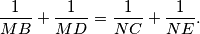
 such that
such that 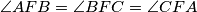 . Let the lines
. Let the lines 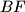 and
and 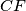 meet the sides
meet the sides  at
at 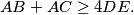
 of five points in the plane, no three of which are collinear, let
of five points in the plane, no three of which are collinear, let 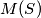 and
and 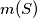 denote the greatest and smallest areas, respectively, of triangles determined by three points from
denote the greatest and smallest areas, respectively, of triangles determined by three points from 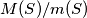 ?
?  and
and 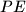 and
and 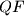 intersect on the circumcircle of triangle
intersect on the circumcircle of triangle 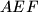 .
. and
and  , respectively. Let
, respectively. Let  be the point where the lines
be the point where the lines 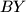 and
and 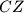 meet, and let
meet, and let  and
and 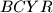 and
and 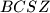 are parallelogram.
are parallelogram.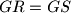 .
.