Let
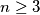
be a positive integer. Let
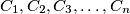
be unit circles in the plane, with centres
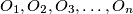
respectively. If no line meets more than two of the circles, prove that
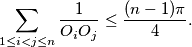
%V0
Let $n\geq3$ be a positive integer. Let $C_1,C_2,C_3,\ldots,C_n$ be unit circles in the plane, with centres $O_1,O_2,O_3,\ldots,O_n$ respectively. If no line meets more than two of the circles, prove that $$\sum\limits^{}_{1\leq i<j\leq n}{1\over O_iO_j}\leq{(n-1)\pi\over 4}.$$