Let

be a positive integer and let
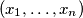
,
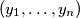
be two sequences of positive real numbers. Suppose
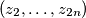
is a sequence of positive real numbers such that
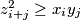
for all
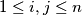
.
Let
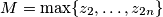
. Prove that
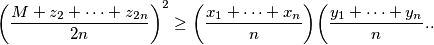
comment
Edited by Orl.
%V0
Let $n$ be a positive integer and let $(x_1,\ldots,x_n)$, $(y_1,\ldots,y_n)$ be two sequences of positive real numbers. Suppose $(z_2,\ldots,z_{2n})$ is a sequence of positive real numbers such that $z_{i+j}^2 \geq x_iy_j \qquad$ for all $1\le i,j \leq n$.
Let $M=\max\{z_2,\ldots,z_{2n}\}$. Prove that
$$\biggl(\frac{M+z_2+\cdots+z_{2n}}{2n}\biggr)^2\ge \biggl(\frac{x_1+\cdots+x_n}{n}\biggr)\biggl(\frac{y_1+\cdots+y_n}{n}\biggr...$$
comment
Edited by Orl.