Slični zadaci
Let 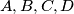 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 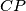 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 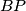 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 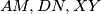 are concurrent.
are concurrent.
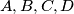 be four distinct points on a line, in that order. The circles with diameters
be four distinct points on a line, in that order. The circles with diameters  and
and  intersect at
intersect at  and
and  . The line
. The line  meets
meets  at
at  . Let
. Let  be a point on the line
be a point on the line  other than
other than  . The line
. The line 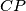 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  , and the line
, and the line 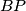 intersects the circle with diameter
intersects the circle with diameter  at
at  and
and  . Prove that the lines
. Prove that the lines 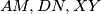 are concurrent.
are concurrent. We are given a positive integer  and a rectangular board
and a rectangular board  with dimensions
with dimensions 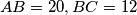 . The rectangle is divided into a grid of
. The rectangle is divided into a grid of 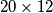 unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is
unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is 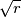 . The task is to find a sequence of moves leading from the square with
. The task is to find a sequence of moves leading from the square with  as a vertex to the square with
as a vertex to the square with  as a vertex.
as a vertex.
(a) Show that the task cannot be done if is divisible by 2 or 3.
is divisible by 2 or 3.
(b) Prove that the task is possible when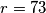 .
.
(c) Can the task be done when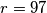 ?
?
 and a rectangular board
and a rectangular board  with dimensions
with dimensions 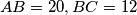 . The rectangle is divided into a grid of
. The rectangle is divided into a grid of 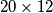 unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is
unit squares. The following moves are permitted on the board: one can move from one square to another only if the distance between the centers of the two squares is 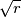 . The task is to find a sequence of moves leading from the square with
. The task is to find a sequence of moves leading from the square with  as a vertex to the square with
as a vertex to the square with  as a vertex.
as a vertex. (a) Show that the task cannot be done if
 is divisible by 2 or 3.
is divisible by 2 or 3. (b) Prove that the task is possible when
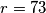 .
. (c) Can the task be done when
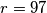 ?
?  Školjka
Školjka  ,
,  be the feet of the perpendiculars from
be the feet of the perpendiculars from  to the lines
to the lines  ,
,  , respectively. Show that
, respectively. Show that 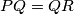 if and only if the bisectors of
if and only if the bisectors of 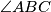 and
and 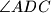 are concurrent with
are concurrent with 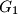 and
and 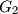 intersect at two points
intersect at two points  be the line parallel to
be the line parallel to  ; lines
; lines 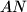 and
and 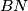 and
and 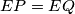 .
.  be an integer. Let
be an integer. Let 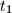 ,
, 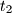 , ...,
, ..., 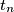 be positive real numbers such that
be positive real numbers such that 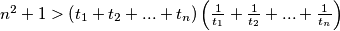 .
. 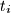 ,
, 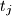 ,
, 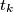 are side lengths of a triangle for all
are side lengths of a triangle for all  ,
,  ,
,  with
with 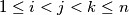 .
.  the bisector of angle
the bisector of angle 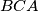 intersects the circumcircle again at
intersects the circumcircle again at  and the midpoint of
and the midpoint of  . Prove that the triangles
. Prove that the triangles 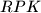 and
and 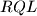 have the same area.
have the same area. 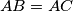 . The angle bisectors of
. The angle bisectors of 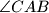 and
and 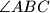 meet the sides
meet the sides 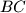 and
and 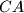 at
at 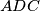 . Suppose that
. Suppose that 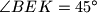 . Find all possible values of
. Find all possible values of