Let  be a triangle with semiperimeter
be a triangle with semiperimeter  and inradius
and inradius  . The semicircles with diameters
. The semicircles with diameters  ,
,  ,
,  are drawn on the outside of the triangle
are drawn on the outside of the triangle  . The circle tangent to all of these three semicircles has radius
. The circle tangent to all of these three semicircles has radius  . Prove that
. Prove that
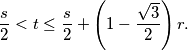
Alternative formulation. In a triangle , construct circles with diameters
, construct circles with diameters  ,
,  , and
, and  , respectively. Construct a circle
, respectively. Construct a circle  externally tangent to these three circles. Let the radius of this circle
externally tangent to these three circles. Let the radius of this circle  be
be  .
.
Prove: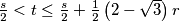 , where
, where  is the inradius and
is the inradius and  is the semiperimeter of triangle
is the semiperimeter of triangle  .
.
 be a triangle with semiperimeter
be a triangle with semiperimeter  and inradius
and inradius  . The semicircles with diameters
. The semicircles with diameters  ,
,  ,
,  are drawn on the outside of the triangle
are drawn on the outside of the triangle  . The circle tangent to all of these three semicircles has radius
. The circle tangent to all of these three semicircles has radius  . Prove that
. Prove that 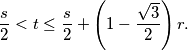
Alternative formulation. In a triangle
 , construct circles with diameters
, construct circles with diameters  ,
,  , and
, and  , respectively. Construct a circle
, respectively. Construct a circle  externally tangent to these three circles. Let the radius of this circle
externally tangent to these three circles. Let the radius of this circle  be
be  .
. Prove:
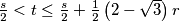 , where
, where  is the inradius and
is the inradius and  is the semiperimeter of triangle
is the semiperimeter of triangle  .
.  Školjka
Školjka