Let

be a fixed integer greater than

. The sequence
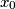
,
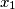
,
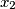
,

is defined as follows:
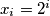
if
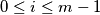
and
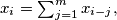
if
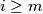
.
Find the greatest

for which the sequence contains

consecutive terms divisible by

.
%V0
Let $m$ be a fixed integer greater than $1$. The sequence $x_0$, $x_1$, $x_2$, $\ldots$ is defined as follows:
$x_i= 2^i$ if $0 \leq i\leq m-1$ and $x_i = \sum_{j=1}^{m}x_{i-j},$ if $i\geq m$.
Find the greatest $k$ for which the sequence contains $k$ consecutive terms divisible by $m$.