Slični zadaci
Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 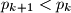 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 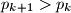 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 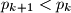 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 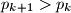 .
. We define a sequence 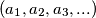 by setting
by setting
![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 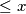 ).
).
a) Prove that there is an infinite number of positive integers such that
such that 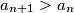 .
.
b) Prove that there is an infinite number of positive integers such that
such that 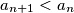 .
.
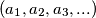 by setting
by setting ![a_{n} = \frac {1}{n}\left(\left[\frac {n}{1}\right] + \left[\frac {n}{2}\right] + \cdots + \left[\frac {n}{n}\right]\right)](/media/m/0/f/c/0fcd7236589e4454f518b8d8aa9fe147.png)
for every positive integer
 . Hereby, for every real
. Hereby, for every real  , we denote by
, we denote by ![\left[x\right]](/media/m/3/6/9/3697c66f8530757a1166f24a1fd325e6.png) the integral part of
the integral part of  (this is the greatest integer which is
(this is the greatest integer which is 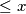 ).
). a) Prove that there is an infinite number of positive integers
 such that
such that 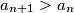 .
. b) Prove that there is an infinite number of positive integers
 such that
such that 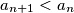 .
.  Školjka
Školjka  be a fixed integer greater than
be a fixed integer greater than  . The sequence
. The sequence 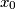 ,
,  ,
, 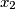 ,
,  is defined as follows:
is defined as follows: 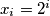 if
if 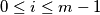 and
and 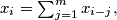 if
if 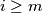 .
.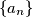 je zadan na ovaj način:
je zadan na ovaj način: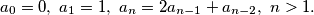
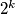 dijeli
dijeli  ako i samo ako
ako i samo ako  ,
,  , ...,
, ..., 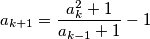 for every
for every 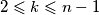 .
.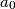 ,
, 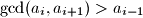 . Prove that
. Prove that 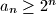 for all
for all 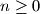 .
.  be an integer greater than
be an integer greater than  . For each positive integer
. For each positive integer 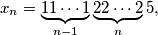
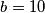 : there exists a positive integer
: there exists a positive integer  such that for any integer
such that for any integer 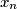 is a perfect square.
is a perfect square.